向量(vector)

1.向量

向量可以理解为空间中的一条线段。
当你加上一个坐标轴，将线段的一端摆到坐标轴的原点，那么便可以通过一个坐标(x,y,z)去表示这个向量。

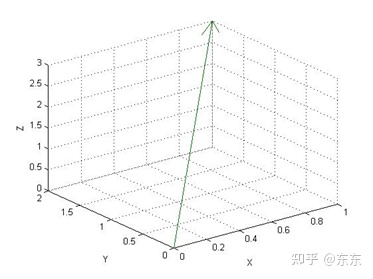
向量的表示方式

但是向量一般用以下方式表示：

$\left|\begin{array}{c}x\\ y\\ z\end{array}\right|$

或者用：$[xyz{]}^T$，意思是将[x,y,z]行转列。

向量的运算

【向量的相加】

$\left|\begin{array}{c}1\\ 2\\ 3\end{array}\right|+\left|\begin{array}{c}1\\ 1\\ 1\end{array}\right|=\left|\begin{array}{c}1+1\\ 2+1\\ 3+1\end{array}\right|=\left|\begin{array}{c}2\\ 3\\ 4\end{array}\right|$

用图形表示则如下：

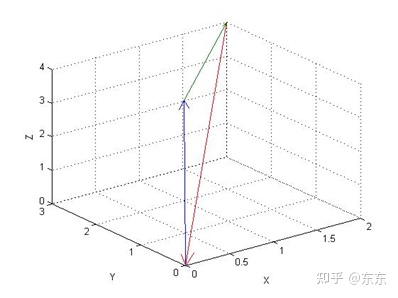
向量的相加，等于向量对应的两条线段首尾相连，形成的一个新的向量。

 
 
 
 
 
【向量的数乘】

$\left|\begin{array}{c}1\\ 2\\ 3\end{array}\right|\times 2=\left|\begin{array}{c}1\times 2\\ 2\times 2\\ 3\times 2\end{array}\right|=\left|\begin{array}{c}2\\ 4\\ 6\end{array}\right|$

向量的数乘，等于向量在原有向量方向上伸长或缩短，方向不变。

向量的相加、数乘也被称为向量的线性运算。

 
 
 
 
 
【向量的点乘(dot product)】

又名点积、数量积。点积的定义又分为代数定义和几何定义。

对于向量a = (x1,y1),b =(x2,y2)：
 
 
代数定义：
$\overrightarrow{a}\cdot \overrightarrow{b}=x_1{x}_2+y_1{y}_2$

 
 
几何定义：
$\overrightarrow{a}\cdot \overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}||\cos \theta |$
可以理解为：向量a的长度 乘以 向量b投影到向量a上的长度
 
 

点积满足交换律、分配律以及结合律。

• 交换律：$\overrightarrow{a}\cdot \overrightarrow{b}=\overrightarrow{b}\cdot \overrightarrow{a}$
• 分配律：$\overrightarrow{a}\cdot (\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}\cdot \overrightarrow{b}+\overrightarrow{a}\cdot \overrightarrow{a}$
• 结合律：$(m\overrightarrow{a})\cdot \overrightarrow{b}=\overrightarrow{a}\cdot (m\overrightarrow{b})$

2.向量的基(basis)

当去掉坐标轴后，是不是就无法表示向量呢？这里又引入向量的“基”(basis)这个概念。

在去掉坐标轴之前，我们以x轴、y轴、z轴为向量方向，以1为向量长度，生成3个向量：

$e1=\left|\begin{array}{c}1\\ 0\\ 0\end{array}\right|$ ，$e2=\left|\begin{array}{c}0\\ 1\\ 0\end{array}\right|$ ，$e3=\left|\begin{array}{c}0\\ 0\\ 1\end{array}\right|$

这3个向量又叫单位方向向量。

此时，$v1=[1,2,3{]}^T$这个向量就可以用这3个向量表示：

$1\times \left|\begin{array}{c}1\\ 0\\ 0\end{array}\right|+2\times \left|\begin{array}{c}0\\ 1\\ 0\end{array}\right|+3\times \left|\begin{array}{c}0\\ 0\\ 1\end{array}\right|=\left|\begin{array}{c}1\\ 2\\ 3\end{array}\right|$

e1,e2,e3就可以称为v1的一组基(basis)。它们代替坐标轴作为v1的参照物。

向量可以有很多组基，在不同的基下，向量的数字定义也不一样。

例如以e1,e2,e3作为基，v1的数字定义为$v1=[1,2,3{]}^T$；

但如果e1换成$v1=[-1,0,0{]}^T$，那么v1的数字定义就会变为$v1=[-1,2,3{]}^T$。

3.向量的张成(span)

（1）对向量c1：$\left|\begin{array}{c}1\\ 2\\ 3\end{array}\right|$ 作任意数乘，可以得到新的向量；这些向量组成的集合，称为c1的张成(span)；

用几何定义来表示，可以看见，这个张成实质就是c1所在的一条直线：

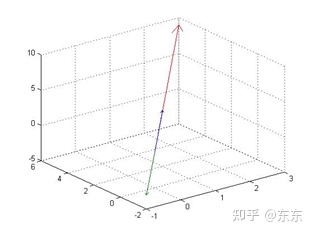
（2）对两个向量c1：$\left|\begin{array}{c}1\\ 2\\ 3\end{array}\right|$ d1：$\left|\begin{array}{c}1\\ 1\\ 1\end{array}\right|$ ，作任意相加和数乘运算，可以得到新的向量；这些向量组成的集合，称为c1,d1的张成(span)；

用几何定义来表示，可以看见，这个张成实质就是一个平面：

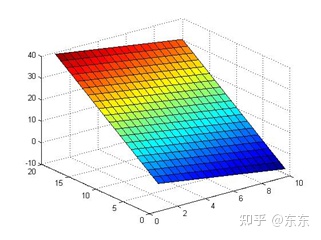
（3）对第2节中的单位方向向量e1,e2,e3作任意相加和数乘运算，我们可以想象得到，它们的张成就是整个空间；

向量空间

略

4.向量的线性相关&线性无关

假设有以下3组向量：

$e1=\left|\begin{array}{c}1\\ 2\\ 3\end{array}\right|$ ，$e2=\left|\begin{array}{c}1\\ 1\\ 1\end{array}\right|$ ，$e3=\left|\begin{array}{c}3\\ 5\\ 7\end{array}\right|$

你会发现，这3组向量形成的张成是一个平面，而不是整个空间。
 
 
 
 

为什么会产生这种情况？原因是：

$2\times \left|\begin{array}{c}1\\ 2\\ 3\end{array}\right|+\left|\begin{array}{c}1\\ 1\\ 1\end{array}\right|=\left|\begin{array}{c}3\\ 5\\ 7\end{array}\right|$

即 $[3,5,7{]}^T$这个向量可以用$[1,2,3{]}^T$以及$[1,1,1{]}^T$ 通过线性运算（向量的相加以及数乘）计算出来，则$[3,5,7{]}^T$这个向量是多余的，用2个向量与3个向量的效果是一样的。
此时，我们称这3个向量线性相关。

 
 
 
 
 
反之，$[1,2,3{]}^T$以及$[1,1,1{]}^T$这两个向量不能通过相加以及数乘去表示对方，我们则称这两个向量线性无关。

 
 
 
 
 
换一种说法：
线性相关的向量，满足 $2\times \left|\begin{array}{c}1\\ 2\\ 3\end{array}\right|+\left|\begin{array}{c}1\\ 1\\ 1\end{array}\right|-\left|\begin{array}{c}3\\ 5\\ 7\end{array}\right|=0$
而线性无关的向量，只有 $0\times \left|\begin{array}{c}1\\ 2\\ 3\end{array}\right|+0\times \left|\begin{array}{c}1\\ 1\\ 1\end{array}\right|=0$

 
 
 
 
 
因此，我们可以得出线性相关的数学定义：
对于向量空间$V$ 中的一组向量$v_1,v_2...v_m$ ，如果使得$a_1{v}_1+a_2{v}_2+...a_m{v}_m=0$ 的系数$a_1,a_2...a_m$ 只有$a_1=a_2=...=a_m=0$ 时才成立，则称$(v_1,v_2...v_m)$这组向量是线性无关的。

4.1 线性相关的定理

定理1 a1,a2,...,an 线性相关的 充分必要条件 为：至少一个向量可由其他向量线性表示。

定理2 a1,a2,...,an 线性无关，但a1,a2,...,an,b线性相关，则b可由a1,a2,...,an唯一表示。

定理3 【替换定理】a1,a2,...,an 线性无关，可由b1,b2,...,bm表示，则m>=n

定理4 n+1个n维向量必线性相关

定理5 等价的线性无关的向量组向量个数相同

5.单位正交基

我们知道什么是线性相关了，此时我们可以重新定义一下基(basis)：

若向量空间$V$ 中有一个向量组既线性无关又张成$V$ ，则称之为$V$ 的一组基。

通常我们研究的基都是单位长度且正交的。

• 单位长度：指的是每个基向量的矢量长度为1。
• 正交：这组基中任意两个向量点乘为零。

当然，基也可以不是单位长度，不是正交的，只是单位正交基比较方便我们研究向量。

6.基变换

在第2节中，我们看到向量在不同的基下的数学定义是不一样的。

就好像我们跑步时，用不同事物作为参照物，我们跑步的快慢看起来也不一样。

在单位正交基$[1,0{]}^T$,$[0,1{]}^T$下，有一个向量a1的数学定义为 $[8,3{]}^T$；

当它在另一组单位正交基$[\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}{]}^T$，$[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}{]}^T$下，它的数学定义又是多少呢？如何转换？

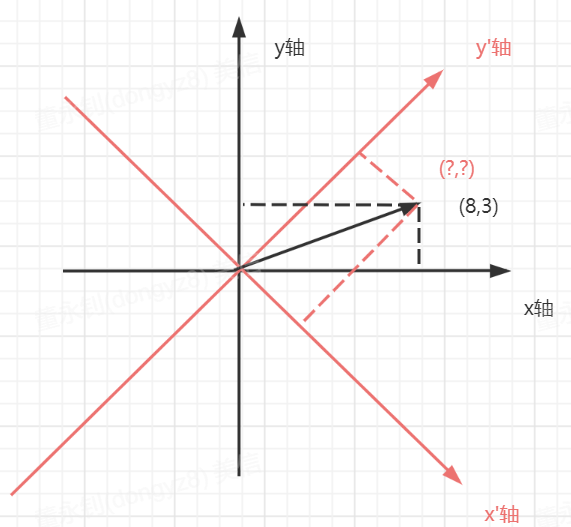
很简单，从图中我们可以看出：

1. 用a1 与 $[\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}{]}^T$做点乘，可以得到a1在x'轴上的值；
   $[8,3{]}^T\cdot [\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}{]}^T=8\times \frac{1}{\sqrt{2}}+3\times -\frac{1}{\sqrt{2}}=\frac{5}{\sqrt{2}}$

2. 用a1 与 $[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}{]}^T$ 做点乘，可以得到a1在y'轴上的值；
   $[8,3{]}^T\cdot [\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}{]}^T=8\times \frac{1}{\sqrt{2}}+3\times \frac{1}{\sqrt{2}}=\frac{11}{\sqrt{2}}$

3. 结合1和2，得到向量a1在新基上的数学定义:$[\frac{5}{\sqrt{2}},\frac{11}{\sqrt{2}}{]}^T$

这种转换就叫基变换。

基变换的矩阵表示

略

7.向量组的秩

极大无关组

有以下向量组：$a1=[1,0{]}^T$、$a2=[2,0{]}^T$、$a3=[0,5{]}^T$、$a4=[0,10{]}^T$

我们可以看到，a2可由a1表示（线性相关），a4可由a3表示。
因此，a2、a4其实是信息冗余的。
此时，我们称a1、a3为这个向量组的极大无关组。

性质：

1. 极大无关组中的向量线性无关；
2. 向量组中每个向量均可由极大无关组中的向量组合表示；

向量组的等价

定义：

1. 两个向量组维度相同
2. A中的向量可由B中向量通过线性计算得到，则称A、B向量组是等价的。
3. 两个等价的线性无关的向量组所含向量的个数相同。
4. 等价的向量组的秩相同，但是秩相同的向量组不一定等价。

性质：

1. 反身性（自己与自己等价）： $A\cong A$
2. 对称性（可以反过来写）： 若$A\cong B$，则有$B\cong A$
3. 传递性：若$A\cong B$，$B\cong C$，则有$A\cong C$

向量组的秩定义

极大无关组含向量的个数，就是该向量组的秩。记作r(a1,a2...,an)

注意：

1. 0 <= r(a1,a2,...,an) <= min{向量的个数，向量的维数}
2. a1,a2,...,an线性无关 等价于 r(a1,a2,...,an) = 向量的个数
3. a1,a2,...,an线性相关 等价于 r(a1,a2,...,an) < 向量的个数

矩阵的行秩、列秩

【行秩】
我们将一个矩阵的每一行都看成一个向量，则我们可以得到一个行向量组。
这个行向量组的秩，就称作这个矩阵的行秩。

【列秩】
我们将一个矩阵的每一列都看成一个向量，则我们可以得到一个列向量组。
这个列向量组的秩，就称作这个矩阵的列秩。

定理1：矩阵的行秩 = 矩阵的列秩 = 矩阵的秩
定理2：r(AB) <= min{r(A),r(B)}
定理3：初等行变换不改变矩阵列向量组的线性关系

什么是向量组的线性关系？

求向量组的秩

步骤：

1. 将向量组按列构成一个矩阵
2. 只通过初等行变换，化成行简化阶梯型矩阵
3. 首非零元所在列，作为极大线性无关组
4. 剩下的列的表示系数即为简化阶梯型矩阵上对应的系数

例题：

求以下向量组的极大线性无关组，并用极大线性无关组表示向量组中的其他向量。

$a_1=[1,-2,2,-1{]}^T$
$a_2=[2,-4,8,0{]}^T$
$a_3=[-2,4,-2,3{]}^T$
$a_4=[3,-6,0,-6{]}^T$

解答：

1. 按列排成矩阵

$\left(\begin{array}{cccc}1& 2& -2& 3\\ -2& -4& 4& 6\\ 2& 8& -2& 0\\ -1& 0& 3& 6\end{array}\right)$

2. 通过初等行变换，将矩阵转换成简化阶梯型矩阵

$\left(\begin{array}{cccc}1& 0& -3& 6\\ 0& 1& \frac{1}{2}& -\frac{3}{2}\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$

3. 首非零元所在列，作为极大线性无关组

$b_1=[1,0,0,0{]}^T$
$b_2=[0,1,0,0{]}^T$

即$b_1$,$b_2$为向量组的极大线性无关组

4. 剩下的列的表示系数即为简化阶梯型矩阵上对应的系数

剩下的两列：

$b_3=[-3,\frac{1}{2},0,0{]}^T$
$b_4=[6,-\frac{3}{2},0,0{]}^T$

可以直接用极大无关组乘以对应系数表示。

$b_3=-3\times b_1+\frac{1}{2}\times b_2$
$b_4=6\times b_1-\frac{3}{2}\times b_2$

最后，原向量组的线性关系，与初等行变换之后的向量组的线性关系是一样的。

$a_3=-3\times a_1+\frac{1}{2}\times a_2$
$a_4=6\times a_1-\frac{3}{2}\times a_2$